1. 목차
최소 스패닝 트리 (MST)
핵심 코드
2. 최소 스패닝 트리 (MST)
최소 스패닝 트리는 주어진 연결된 그래프에서 모든 정점을 포함하면서 그래프의 모든 정점을 연결하는 간선의 부분 집합 중에서 가중치의 합이 최소인 트리를 말합니다.
최소 스패닝 트리를 찾는 알고리즘은 크게 두 가지가 있습니다. 그중 크루스칼 알고리즘에 대하여 알아보겠습니다.

위와 같이 연결된 그래프에서 크루스칼 알고리즘을 통하여 MST를 구하는 방법을 알아보겠습니다.
각 Node와 연결되는 간선의 정보를 배열에 저장합니다. ex) Edge {A, B, 1}
각 Node의 부모 노드를 판별하기 위한 Parent 배열을 생성합니다. (Node의 알파벳을 각 번호로 변)
초기 값은 자기 자신을 부모로 지정합니다.
크루스칼 알고리즘을 통한 최소 경로를 가지는 트리를 확인하는 방법은 간선의 가중치가 가장 낮은 간선을 먼저 확인하는 것입니다.
간선 정보를 저장한 배열을 가중치를 기준으로 정렬을 합니다.
정렬 후 totalWeight를 찾는 과정은 아래와 같습니다.
각 노드의 부모 값을 확인하고 서로의 부모가 다르다면 부모 값을 통일하여 연결되어 있다는 것을 기록하고 totalWeight를 증가시킵니다.
<bash />
for i:=0 ; i <len(EdgeList) ; i++ {
fromRoot := FindRoot(EdgeList[i].from, Parent)
toRoot := FindRoot(EdgeList[i].to, Parent)
if fromRoot != toRoot {
Parent[fromRoot] = toRoot
totalWeight += EdgeList[i].value
}
}
EdgeList
| A,B | E,G | B,C | E,F | B,D | C,F | G,H | C,E | F,H | D,E |
| 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 5 | 6 |
Parent
| A(1) | B(2) | C(3) | D(4) | E(5) | F(6) | G(7) | H(8) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Edge의 첫 번째 값을 확인하여 두 Node의 부모를 확인 후 다르다면 A의 Parent를 B의 Parent로 변경합니다.
간선의 값만큼 전체 가중치를 증가시킨다.

totalValue = 1
Parent
| A(1) | B(2) | C(3) | D(4) | E(5) | F(6) | G(7) | H(8) |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
다음 Edge의 값을 확인하여 E와 G Node를 대상으로 동일한 작업을 진행합니다.

totalValue = 2
Parent
| A(1) | B(2) | C(3) | D(4) | E(5) | F(6) | G(7) | H(8) |
| 2 | 2 | 3 | 4 | 7 | 6 | 7 | 8 |
B와 C도 같은 작업을 한 후 E와 F를 확인해 보면 E의 부모는 G이고 F의 부모는 F이므로 값이 다르기에 E의 부모의 부모 즉 G의 부모를 F로 지정합니다.

totalValue = 6
Parent
| A(1) | B(2) | C(3) | D(4) | E(5) | F(6) | G(7) | H(8) |
| 2 | 3 | 3 | 4 | 7 | 6 | 6 | 8 |
이러한 과정이 반복되면 최종적으로 연결된 간선과 Parent의 값은 아래와 같습니다.
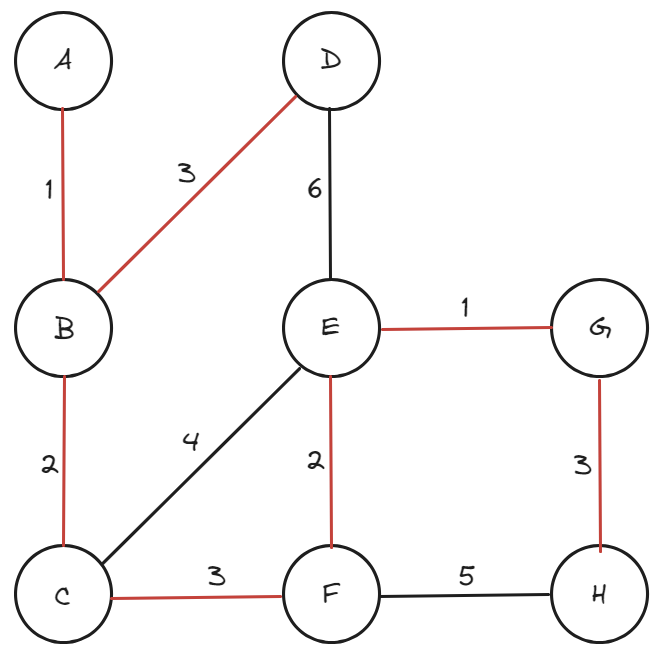
totalValue = 15
Parent
| A(1) | B(2) | C(3) | D(4) | E(5) | F(6) | G(7) | H(8) |
| 2 | 3 | 4 | 6 | 7 | 6 | 6 | 6 |
위의 상황에서 연결되지 않은 간선의 경우 연결을 시도하게 되면 부모의 값이 동일하다는 결과가 나옵니다.
C의 최 상위 부모 : F(6) C->D->F
E의 최 상위 부모 : F(6) E->G->F
위의 방법을 통하여 MST를 구할 수 있었습니다.
3. 핵심 코드
간선 연결 Process
<bash />
func Process(V int, EdgeList []Edge) int {
Parent := make([]int, V+1)
for i:=1 ; i<=V ; i++ {
Parent[i]=i
}
sort.Slice(EdgeList, func(i, j int)bool {return EdgeList[i].value < EdgeList[j].value})
var totalWeight int
for i:=0 ; i <len(EdgeList) ; i++ {
fromRoot := FindRoot(EdgeList[i].from, Parent)
toRoot := FindRoot(EdgeList[i].to, Parent)
if fromRoot != toRoot {
Parent[fromRoot] = toRoot
totalWeight += EdgeList[i].value
}
}
return totalWeight
}
FindRoot
<bash />
func FindRoot(num int, Parent []int) int {
if Parent[num] == num {
return Parent[num]
}
Parent[num] = FindRoot(Parent[num], Parent)
return Parent[num]
}'Computer Science' 카테고리의 다른 글
| [Storage] Object Storage (0) | 2024.07.27 |
|---|---|
| [CS] 다익스트라 알고리즘 (Dijkstra) (0) | 2023.10.25 |
| [CS] 데이터 직렬화 (marshaling과 unmarshaling) (0) | 2023.09.22 |
| [CS] Blocking과 NonBlocking, Sync와 Async 공부 기록 (0) | 2023.07.22 |
| [CS] 그래프 알고리즘 (깊이 우선 탐색, 너비 우선 탐색) (0) | 2023.06.22 |

